Missing bit solution

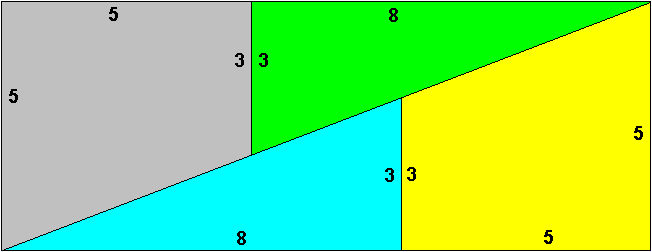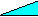
The hint tells you to look carefully at the second diagram, shown on the left. Its area is 65 square units, but are you sure that these shapes will fit together in this way? The triangle and the trapezium certainly can lie side by side, since they both have one side of 3 units, but it takes more than sides in common to fit shapes together.

Let's start by drawing an accurate diagram.

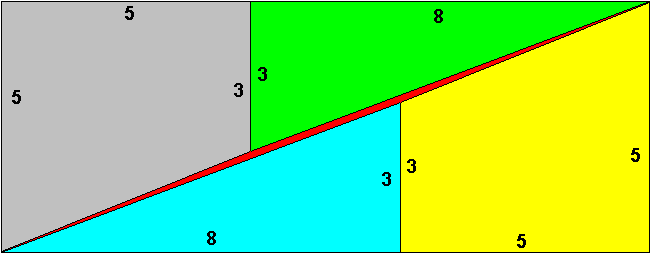I copied the triangles and the trapeziums from the original diagram, and tried to fit them together.

Aha! They don't fit! There is a thin sliver between them (coloured red). That is where our missing bit comes from.

Can we work this out logically rather than by drawing an accurate diagram? After all, the diagram doesn't tell us what went wrong.

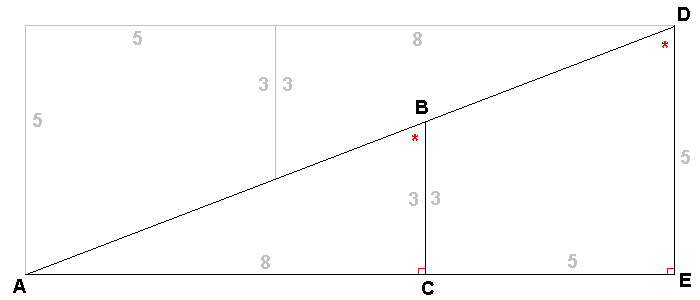I've reproduced the original diagram (making bits grey where I'm not really interested in them) and labelled various points. This diagram thinks that the line AD is a straight line. Is it? The lines BC and DE are parallel (since they cross the line CE at right angles, marked in red). If AD is straight, then the angles ABC and BDE (marked as *) are the same size.

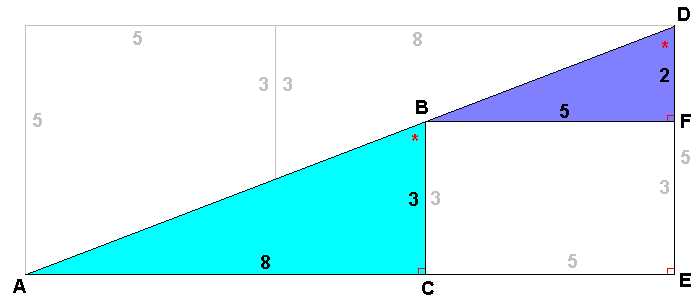I've drawn an extra triangle BDF by drawing a line at right angles to DE to meet point B. BF is 5 units (because CEFB is a rectangle) and DF is 2 units (= 5 - 3). Now we see the problem. If angles ABC = angle BDE, then triangle ABC should be similar to BFD (since they have all three angles the same: the angle we're talking about, a right angle, and angles of a triangle must add up to 180 degrees.) That means that their sides must be in proportion. But 3/8 is not the same as 2/5. So the triangles are not similar. So the angles are not the same, and the diagram is wrong.